Swing traders often choose stocks to trade because, in addition to the thousands of publicly traded companies available, a growing number of exchange-traded funds (ETFs) are also available. These ETFs trade just like corporate stocks, and stock exchanges now offer the opportunity to trade a wide variety of other markets, including commodities, currencies, indexes, leveraged and inverse instruments, as well as foreign markets. For the purpose of this article, “stocks” will include all these instruments that trade like stocks. Successful swing traders use a disciplined approach to trade a back-tested system, and often select a small number of stocks to trade from the thousands that are available. Trading can involve risks if not done with right knowledge and experience. TrustedBrokers.com can be of help in this case.
There are a number of factors to consider when selecting which stocks to trade. A couple of obvious considerations are price and liquidity. Price is important because it determines the number of shares or option contracts that can be traded in order to commit the desired capital and allocate the appropriate risk. Liquidity is important for determining the ease of trade entry and exit, and for reducing transaction costs associated with bid/ask spreads. But another often-overlooked consideration is volatility. Since swing traders expect to be in a trade from a day or two to a few days to a few weeks, the expected move a stock is very important. Volatility provides a measurement of how much a stock price moves, and is important because it gives us an indication as to whether or not our price targets and stops are reasonable and our risk parameters are acceptable for the period of time we expect to be in our trade. This article will examine a couple of metrics used for measuring historical and future volatility.
First, let’s define volatility. Volatility is a measure of the relative rate at which the price of a stock moves up or down over a specific period of time. It represents the amount of uncertainty about the magnitude and direction of the price change of a stock. A higher volatility means that a stock price can potentially move over a larger range of values, and that the price of the stock can change dramatically over a short time period in either direction. A lower volatility means that a stock’s price does not fluctuate as dramatically, and we can expect smaller price changes over a period of time. Traditionally, high volatility stocks are considered “riskier”, but swing traders often seek out these stocks with the expectation of achieving higher returns. There are a number of ways to measure the volatility of a stock.
One measure of the volatility of a particular stock is its beta. Beta measures the approximate overall volatility of a security’s returns against the returns of a relevant benchmark, usually the S&P 500. For example, a stock with a beta value of 1.0 has historically moved 100% for every 100% move in the benchmark. The SPY has a beta of 1.0 because this ETF attempts to exactly track the performance of the S&P 500. A stock with a beta of 1.2 has historically moved 120% of the move of the S%P 500. Conversely, a stock with a beta of 0.8 has historically moved 80% of the move in the S&P 500. Betas can also be negative, and can even have absolute values greater that 100%. For instance, a double-leveraged ETF that attempts to track the inverse of the S&P would have a beta of -2.0. In this case, with a 10% drop in the S&P we would expect the price of this ETF to rise by 20%. Stock betas can provide a useful guideline for selecting stocks to swing trade, and swing traders tend to select stocks with betas greater than 1.0 (such as most tech stocks), but beta alone may not always be useful because the correlation to the relevant benchmark may not be consistent: stocks with a positive beta can still fall when the S&P rises. Also, some stocks may exhibit volatile price swings, but do not correlate well to any benchmark index. Another issue with beta is that the correlation to the S&P 500 (or other index) can change over time, and since beta is based on historical data, it may not accurately reflect future price moves.
Another measure of a stock’s volatility is its historical volatility and its implied volatility. These values are not dependent upon a benchmark, and are calculated using only the price of the individual stock. The time frame that is most often used is one year, and is therefore referred to as annual volatility. (When no time frame is given, the volatility of a stock refers to its annual volatility.) Volatility is a mathematical statistic that is determined by measuring daily changes in stock price, and calculating the annualized standard deviation of these daily price changes. In statistics, one standard deviation represents approximately 68% of the area under a bell-shaped curve. As a measure of stock volatility, this represents the range that we can expect the closing price of a stock to be 68% of the time at the end of one year. Historically, the volatility of the stock market is roughly 20%. This means that 68% of the time we can expect the stock market to move up or down 20% a year or less. Individual stocks can have historical volatility higher or lower than the average for the stock market. As of this writing, Apple (AAPL) is trading for $540 and its average annual historical volatility is approximately 30%. This means that using historical averages, there is a 68% chance that one year from now the price of AAPL will be within 30%, or $162, of its current price, or $378 to $702.
As traders we are well aware that stock volatility changes over time, going through periods of high and low volatility where price range may expand or contract. Annual historical volatility can also be calculated using recent price activity, allowing us to calculate annual volatility based on shorter time frames, typically one month. Right now AAPL is trading with an annual volatility of 19%. This means that looking at the recent month’s activity, if AAPL continues to trade with the same volatility that is has recently, then it can be expected to be within 19% of its current price one year from now: up or down only $102. However, in February AAPL was trading with an annual volatility of over 55%, almost three times what it is now. At that time it was trading for $480, and if it continued to trade the same way for the next year, then by the end of one year it would have had expected move of $264.
This is all well and good, but how does this help us trade AAPL or any other stock for that matter, and what good is annual volatility if we are in trades for at most a few weeks? There is another measure of volatility that we can use that makes use of the stock options pricing, known as implied volatility. The options pricing model requires a number of inputs in order to determine the fair price of an option: current stock price, option strike price, days to expiration, interest rates, dividends, and future volatility. At any point in time, all of these inputs are known with certainty, with the exception of future volatility. But since stock options are traded every day in an efficient market, the price of the option determines what the future volatility must be. This is why future volatility is also known as implied volatility: it is implied (calculated) based on all the known inputs plus the actual option market price. The advantage of using implied volatility, instead of historical volatility, is that historical volatility looks only at the past. Implied volatility, as reflected in the option price, lets the marketplace estimate or predict the expected price swings based not only on history, but on all known future events such as earnings announcements, Fed reports, FDA announcements, or other news of concern to traders of the particular stock.
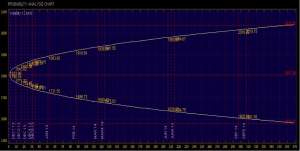
Implied volatility can be found on most broker platforms, and is usually calculated for each option expiration cycle because it is based on the price swings expected by the time the option expires. It is always displayed as an annual number, even if the option is expiring in only a few days. This is why you often see options expiring in a few days with a very high implied volatility right before an earnings announcement – the expected daily price swings are very high on an annualized basis compared with those options expiring in further out months. Traders can make use of these numbers by calculating the expected volatility of a stock for the particular time frame of interest, usually much shorter than a year. The key is knowing which option expiration cycle to select, and how to calculate the implied volatility for the shorter time frame. The best option expiration cycle to select would be the one that has the fewest number of days to expiration that is at least equal to the number of days of interest to the trader. For instance, if a trader is interested in being in a trade for at most 5 days, then it would make sense to look at an the implied volatility for an option that is expiring in 8 days, not the one expiring in 36 days. Most of the time, this is the front month option, or possibly a weekly option. Next, we need to calculate the expected move for the shorter time frame. Since volatility is a statistic calculated using a price that follows a Gaussian random walk, the width of the distribution increases as time increases. However, rather than increase linearly, the volatility increases with the square-root of time. This means that the expected deviation in price after twice the time will not be twice the distance, but will be closer to 1.4 (square root of 2) times the distance. (Time has to quadruple for the expected price deviation to double.) The following chart illustrates this relationship showing the current expected price range for the SPX starting at a value of 1800 with an implied volatility of 12.64%:
Notice that at the end of one year, the expected range of the SPX is about 228 points up or down (0.1264 x 1800). At the end of six months, the expected range of the SPX is about 162 points up or down (0.1264 x 1800 / 1.4).
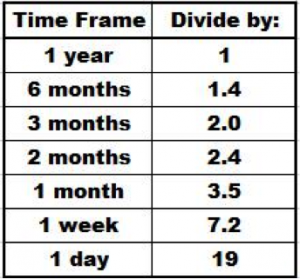
We can easily calculate the expected implied volatility for any time frame by dividing the annual implied volatility by the square root of the ratio of the number of days in a year (365) to the number of days we are interested in being in the trade. For instance, for a month, this would be the square root of 12; for a week, this would be the square root of 52; and for a day this would be the square root of 365. The following chart shows the approximate value to divide annual implied volatility in order to get the implied volatility for some shorter time frames:
This can be very useful for a swing trader to calculate expected price ranges, particularly around news events when implied volatility can rise dramatically, and can be used to assist in managing expectations. For instance, let’s say that you are holding a position in a stock right before an earnings report, and the implied volatility of the front month or weekly option rose to 120%. Knowing this, the trader can make better decisions concerning stops, targets, or whether or not to be in the trade altogether. A one day move in this stock is expected to be about 6.3% (120/19).
Stock swing traders often look only at technical analyses tools and indicators for placing and managing trades, but it can often be very beneficial to look at implied volatility, even if we never trade options, in order to see what range of price swings have been priced-in by the options marketplace. This is particularly useful as we approach important news events, but can be valuable at any time.